Quiz: Fuerzas

1. En un marco de referencia inercial...
   1. Los cuerpos libres no aceleran
   2. Los cuerpos libres tienen cualquier trayectoria
   3. Las leyes de Newton no son válidas
2. Un tren tira de 10 vagones de masa $m$ con una fuerza $F$. Seleccione la suma de fuerzas en el último vagón.
   1. $R=10 ma$
   2. $R = ma$
   3. $R=ma/10$
3. Un tren tira de 10 vagones de masa $m$ con una fuerza $F$. Seleccione la aceleración total del sistema como un todo.
   1. $a=F/(10m) $
   2. $a=10F/m$
   3. $a=F/m$
4. Un tren tira de 10 vagones de masa $m$ con una fuerza $F$. ¿Cuál es la fuerza con la que se tira del último vagón?
   1. $R=10 F$
   2. $R = F$
   3. $R=F/10$
5. Un carro queda varado en el barro. Para sacarlo, se ata una cuerda a un extremo del carro, y el otro extremo, a un árbol. Si para mover el carro se necesitan 1150 N y sabemos que $\theta$=10°, ¿Cuánta fuerza $F$ aplicada a la mitad se necesita para mover el carro?
   
   1. 400 N
   2. 200 N
   3. 1150 N
   Mostrar guía
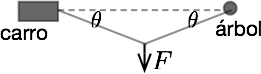
   Haga una suma de fuerzas en el punto de aplicación de $F$. Con eso, encontrará $2T\sin\theta = F$.
6. Un bloque de masa $m$ se desliza sin fricción por un plano inclinado de masa $M$ e inclinación $\theta$. ¿Qué fuerza $F$ horizontal hay que aplicar al plano inclinado para que el bloque no se mueva respecto a la superficie del plano?
   
   1. $F=(m+M)g\tan\theta$
   2. $F=0$
   3. $F=(m+M)g\sin\theta$
   Mostrar guía
   Hay tres ecuaciones que plantear, y con ellas, usted puede resolver el problema. Primera: la suma de fuerzas en el sistema como un todo: $F=(m+M)a$. Segunda y tercera: la suma de fuerzas en el bloque. En $x$, el bloque experimenta una aceleración $a$, pues se mueve con el plano: $N\cos\theta = mg$. En $y$, el bloque no experimenta aceleración, pues queremos que no se deslice hacia abajo: $N\cos\theta - mg = 0$.
Problema: Un bloque de masa $m$ se encuentra sobre una mesa con coeficiente de fricción cinética $\mu_k = 1/2$. Está unido mediante una cuerda a otro bloque de masa $2m$. La polea no tiene masa.

7. ¿Cuál es la tensión de la cuerda?
   1. $T=2mg$
   2. $T=mg$
   3. $T=3mg/2$
8. ¿Cuál es la aceleración del sistema?
   1. $a=g/2$
   2. $a=g$
   3. $a=3g/2$

---

Movimiento circular

9. La fuerza centrífuga...
   1. Se balancea con la centrípeta
   2. Aparece solo en marcos de referencia no inerciales
   3. No existe del todo
10. Si una partícula da 15 vueltas por segundo,
    1. Su periodo es de 15 segundos
    2. Su periodo es de 0.067 segundos
    3. Su periodo es de 15 Hz
11. La Tierra tiene un radio de 6370 km, y da una vuelta cada 24 h. ¿Cuánto afecta al peso $mg$ de una persona la rotación terrestre? Para responder a esta pregunta, recuerde nuestra definición de "peso": esencialmente preguntamos por la fuerza normal en el ecuador.
    1. N=mg
    2. N=0.899mg
    3. N=0.997mg
    Mostrar guía
    Haga una suma de fuerzas en la superficie de la Tierra, en el ecuador: $mr\omega^2=mg-N$. Despeje $N$ y sustituya los valores numéricos. Recuerde que $\omega=2\pi/T$, T=24 h, $g=9.8\unit{m/s^2}$.